1. Programmierparadigmen

Was ist ein Programmierparadigma?

Paradigma steht für Beispiel oder Vorbild
Kontext Programmieren: Programmierstil
Das Erstellen von Code nach vorgegebenen Regeln

Programmierstile:

Imperative Programmierung	Deklarative Programmierung
Wie ist das Problem zu lösen?	Was ist das zu lösende Problem?
Variablen und Wertzuweisungen	Funktionen und formale, mathematische Logik
Anweisungsfolge	Audruck, der ein Ergebnis liefert

Zuordnung:

Imperative Programmierung	Deklarative Programmierung
Prozedurale Programmierung	Funktionale Programmierung
Objektorientierte Programmierung	Logische Programmierung

Prozedurale- vs. Objektorientierte Programmierung

Prozedurale Programmierung	Objektorientierte Programmierung
Denken in Prozeduren	Daten im Mittelpunkt
Für jede Unterscheidung existiert eine eigene Methode	Objekt weiß selber, welche Antwort zu ermitteln ist

2. Typsysteme

Datentyp:

Rechner arbeitet ohne Typen (nur 0 und 1)
Ein Datentyp wird durch die Typisierung von Daten gebildet
Datentypen sind softwareseitige Konstrukte
Ziel: Keine Ausführung falscher Informationen auf eine Bitfolge
Synonym: Typ

Zweck von Typisierung:

Ordnung
Anwendung sinnloser Operationen vermeiden
Typkompatibilität:
- Anwendung eines Operators nur mit korrektem Typ möglich
- Anwendung einer Funktion nur mit korrekten Typen möglich

syntaktische Typkompatibilität	semantische Typkompatibilität
Welche Typbezeichner und Funktionssignaturen stehen zur Verfügung?	liefert eine Funktion das erwartete Ergebnis zurück?
Vorteile: - Unterstützt modulare Entwicklung
- Nutzung neuer Datentypen, wie vordefinierte Datentypen
Nachteil: Syntaktisch Korrekte Implementierung kann semantisch falsch sein

Typsysteme

Es gibt zwei unterschiedliche Typsysteme:

Typangabe ist bei der Dekleration erforderlich:

//Beispiel in Java
int i; // Java

//Beispiel in Pascal
var i: integer;

Typangabe kann aus der Verwendung abgeleitet werden (Typinferenz)
```
//Beispiel in Clojure
(def pi 3.14159)
```

Statische vs dynamische Typisierung

statische Typisierung	dynamische Typisierung
Typprüfung erfolgt zur Übersetzungszeit	Typprüfung folgt während der Ausführung des Programms
Bsp: `Java, C++, C#`	Bsp: `Python, Perl, Php, Smalltalk`

Strenges vs schwaches Typsystem

strenge Typsysteme	schwache Typsysteme
stellt Typensicherheit jederzeit sicher	lässt gelegentlich auch typfremde Operationen zu

Explizites vs implizites Typsystem

explizite Typsysteme	implizite Typsysteme
verlangt für jede Variable die Angabe eines Typs	verlangt die Dekleration einer Variable und leitet den Typ der anderen aus der Verwendung ab

Übersicht Typsysteme

	statisches Typsystem	dynamisches Typsystem `Prolog`
strenges Typsystem	implizites Typsystem `Haskell, Standard ML`	implizites Typsystem `Lisp, Clojure, Smalltalk`
	explizites Typsystem `Java`	explizites Typsystem
schwaches Typsystem	implizites Typsystem	implizites Typsystem `Javascript`
	explizites Typsystem `C`	explizites Typsystem

Funktionale Programmiersprachen

Clojure

Lisp Dialekt
strenges, dynamisches, implizites Typsystem
verschiedene Programmierstile (imperativ, funktional, objektorientiert)

REPL (Read-Eval-Print-Loop)

Liest den Ausdruck
Wertet ihn aus
Gibt das Ergebnis zurück

Beispiel-Code

(def filter 
      (fn [praed? lst]
        (cond 
          (empty? lst) () 
          (praed? (first lst))
             (cons (first lst) (filter praed? (rest lst)))
          :else (filter praed? (rest lst)))))

Standard ML

funktionale Programmiersprache
strenges, statisches, implizites Typsystem
Typinferenz
ermöglicht Pattern-Matching

Beispiel-Code:

(* Filter *)
fun filter (praed, lst) =
    if null lst
    then []
    else if praed (hd lst)
    then 
        hd lst :: filter (praed, tl lst)
    else filter (praed, tl lst)
(* Signatur von filter: fn : ('a -> bool) * 'a list -> 'a list *)

(* Lambda Ausdruck *)
fn x => x+1

(* Funktion benennen *)
val twice = (fn x => 2*x)

(* Funktionen mit Rekursion [fun statt fn] *)
fun fac n = 
	if (n=0) 
	then 1 
	else n*(fac (n-1))

(* Funktion mit getypten Parametern *)
fun pow (x:int, y:int) = 
    if y=0
    then 1
    else x * pow(x,y-1)
    
(* Tupel *)
val pair = (1,"abc")

(* Liste {1} *)
1::nil

(* Zugriff auf das erste Listenelement *)
hd list

(* Zugriff auf den Rest der Liste *)
tl list

(* Records [= HashMaps] *)
val car = {make = "Ford", built = 1904}

(* Zugriff auf HashMap-Einträge *)
#make car

(* Summieren von Listpaaren *)
fun sum_pair (a,b) = a + b;

fun sum_pair_list (lst) = 
  if (lst = nil) 
  then 0 
  else sum_pair (hd lst) + sum_pair_list (tl lst);

sum_pair_list [(2,3), (4,5)]; (* =14 *)

(* Extrahieren des ersten Elements von Listpaaren *)
fun get_first (a,b) = a;

fun firsts (lst) = 
  if lst = nil
  then nil
  else get_first (hd lst) :: (firsts (tl lst));

firsts [(2,3), (4,5)];

(* Datumsfunktionen (DD MM YYY) *)
fun ist_frueher (day1 : int*int*int, day2 : int*int*int) =
    (#1 day1) < (#1 day2)
    orelse (((#2 day1) < (#2 day2))
            andalso ((#1 day1) = (#1 day2)))
    orelse (((#3 day1) < (#3 day2))
            andalso ((#2 day1) = (#2 day2))
            andalso ((#1 day1) = (#1 day2)));

ist_frueher ((2,4,2017), (7,6,2017));

fun in_monat (datum:int*int*int, monat) = #2 datum = monat;

in_monat ((2, 6, 2017), 6);

fun kalenderdaten_in_monat (daten: (int*int*int) list, monat : int) = 
  if daten = nil
  then nil
  else in_monat(hd daten, monat) :: kalenderdaten_in_monat (tl daten, monat);

kalenderdaten_in_monat ([(2, 6, 2018), (5, 6, 2017)], 6);

fun contains (value: bool, lst: (bool) list) =
    if lst = nil
    then false
    else 
      if (hd lst) = value
      then true
      else contains (value, tl lst);

fun daten_in_monat (daten: (int*int*int) list, monat: int) = 
  if daten = nil
  then nil
  else 
      if in_monat (hd daten, monat)
      then (hd daten) :: daten_in_monat (tl daten, monat)
      else daten_in_monat (tl daten, monat);

daten_in_monat ([(2, 6, 2018), (5, 9, 2017)], 6);

fun kalenderdaten_in_monaten (daten: (int*int*int) list, monate: (int) list) = 
  if monate = nil
  then nil
  else daten_in_monat(daten, hd monate) @ kalenderdaten_in_monaten(daten, tl monate);

kalenderdaten_in_monaten ([(2, 6, 2018), (5, 6, 2017), (9, 4, 2018), (9, 9, 2018)], [4, 6, 7]);

fun contains_date (date: int*int*int, lst: (int*int*int) list) =
    if lst = nil
    then false
    else 
      if (hd lst) = date
      then true
      else contains_date (date, tl lst);

fun distinct (daten: (int*int*int) list) =
  if daten = nil
  then nil
  else 
      if tl daten = nil
      then (hd daten) :: nil
      else 
        if contains_date (hd daten, tl daten)
        then distinct (tl daten)
        else (hd daten) :: distinct (tl daten);

fun kalenderdaten_in_monaten_2 (daten: (int*int*int) list, monate: (int) list) =
  distinct (kalenderdaten_in_monaten (daten, monate));

distinct (kalenderdaten_in_monaten_2 ([(2, 6, 2018), (5, 6, 2017), (9, 4, 2018), (9, 9, 2018)], [4, 6, 4, 7]));

3. Ausdrucksmittel funktionaler Programmiersprachen

Datentypen

Erstellung neuer Datentypen in SML:

datatype shape =
         Rectangle of real * real
         | Circle of real

Pattern Matching

Unterscheidung von Typen durch muster => ausdruck
Verschiedene Zweige werden durch | getrennt

fun shape_area s =
    case s of
        Rectangle(w, h) => w * h
      | Circle(r) => 3.14159 * r * r

Verwendung von Pattern Matching

Beispiel-Code:

fun sum_list (xs : int list) =
	if xs = nil
	then 0
	else hd(xs) + sum_list(tl xs)
    
fun sum_list xs =
	case xs of
		[] => 0
		| x::xs’ => x + sum_list xs’

datatype exp = Constant of int
                | Negate of exp
                | Add of exp * exp
                | Multiply of exp * exp;

fun eval exp = 
  case exp of
    Constant(i) => i
  | Negate(ex) => ~(eval(ex))
  | Add(sum1, sum2) => eval(sum1) + eval(sum2)
  | Multiply(fac1, fac2) => eval(fac1) * eval(fac2);

eval (Add (Constant 19, Negate (Constant 4)));

fun list_of_constants (lst: exp list) =
  if lst = nil
  then nil
  else
    case hd lst of
      Constant(i) => i :: list_of_constants(tl lst)
    | _ => list_of_constants(tl lst);

list_of_constants [(Add (Constant 19, Negate (Constant 4))), Constant 19, (Constant 5)];

fun get_bigger (a:int, b:int) =
  if a > b
  then a
  else b;

fun largest_constant_helper(lst: int list) =
case lst of
  [] => []
  | c::[] => [c]
  | c::c2::cs' => largest_constant_helper (get_bigger(c, c2) :: cs');

fun largest_constant(lst: exp list) = largest_constant_helper(list_of_constants(lst));

largest_constant [(Add (Constant 19, Negate (Constant 4))), Constant 19, (Constant 5)];

fun number_of_adds (lst: exp list) =
  if lst = nil
  then 0
  else
    case hd lst of
      Add(a,b) => 1 + number_of_adds(tl lst)
    | _ => 0 + number_of_adds(tl lst);

number_of_adds [(Add (Constant 19, Negate (Constant 4))), Constant 19, Constant 5, (Add (Constant 19, Negate (Constant 4)))];

Curryfizierung - partielle Anwendung

(* Bisherige Form von mehreren Parametern *)
fun sorted3_tupled (x,y,z) = z >= y andalso y >= x

(* Curryfizierte Funktion *)
fun sorted3 x y z = z >= y andalso y >= x

Partielle Anwendung:

Aufruf der Funktion mit weniger Argumenten (hier < 3)
wird häufig für Funktionen höherer Ordnung verwendet

(* Funktionen höherer Ordnung *)
val List.map = fn : (’a -> ’b) -> ’a list -> ’b list

val List.filter = fn : (’a -> bool) -> ’a list -> ’a list

val List.foldl = fn : (’a * ’b -> ’b) -> ’b -> ’a list -> ’b

Clojure

Im Gegensatz zu SML: dynamisch getypte Sprache
Prefixnotation
Verwendung der JVM (wird zu bytecode compiliert)

Grundlagen:

// list
'(1  2  3)
// vector
[1  2  3]
// set
#{1  2  3}
// map
{:a  1, :b  2}

// Function
(defn  greet [name] (str  "Hello, " name) )

// Bedingungen
(if (even?  2)
	"even"
	"odd")


(cond 
	(< x 2) "Case 1"
	(< x 10) "Case 2"
	:else  "Case 3")

// Zugriff auf eine Liste
(first (cons a list)) = a
(rest (cons a list)) = list

Beispiel-Code:

(def make-add
	(fn [a]
		(fn [b]
			(+ a b))))

(def make-prepend
  (fn [a]
    (fn [b]
      (cons a b))))

4. Ausgewählte Kapitel

Datenabstraktion

Es gibt keinen Unterschied zwischen Programmen und Daten
Datentypen kann man bauen und damit unabhängig von festgelegten Repräsentationen rechnen

Metazirkulärer Interpreter

Interpreter, der in derselben Sprache geschrieben ist, die er interpretiert
Prozess der Funktionsanwendung durch eval und apply
eval wertet den Ausdruck aus und gibt das Ergebnis zurück
apply erwartet eine Funktion und eine Sequenz von Argumenten und wendet die Funktion auf die Elemente der Sequenz an
Self-evaluation expression: Ausdruck, der sich selbst wieder als Ergebnis hat

Lazy evaluation

auch: call by need oder promises
Use-Case: Das Ergebnis einer aufwendigen Berechnung wird als Parameter benötigt (keinmal oder n-mal). Durch Lazy Evaluation wird der Wert nicht n-mal durchgeführt, sondern einmal und dann zwischengespeichert.

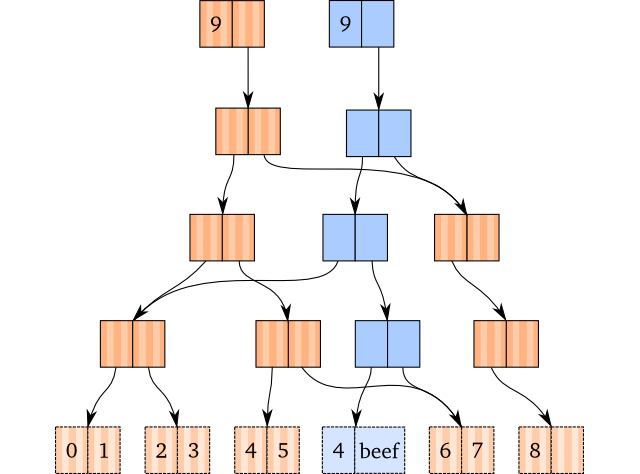
Funktionale Datenstrukturen

Änderungen imperativer Datenstrukturen basieren auf Mutation
Funktionale Datenstrukturen sind nicht änderbar (immutable)
Änderungen von Werten erzeugen ein neues Exemplar der Datenstruktur
Kopien sorgen für eine lange Laufzeit
Lösung: Baumstrukturen, zur Vermeidung von Redundanzen
Bei Änderung eines Werts werden die Knoten des Pfads zum Element kopiert
Verschiedene Fälle sind hier zu finden.
Zur Beschleunigung der Operationen können Mehrwegbäume anstatt von Binärbäumen eingesetzt werden

Beispiel

5. Funktionale- vs. Objektorientierte Programmierung

Funktionale Programmierung	Objektorientierte Programmierung
Fehlen von Mutation	Gebrauch von Mutation
Fehlen von Zuweisungen	Gebrauch von Zuweisungen
Funktionen	Objekte (Funktionen mit internen Daten)
Funktionen	Methoden

Zusammenfassung:

Für eine “objektorientierte Programmierung” bedarf es keiner speziellen Programmiersprache
Objekte sind:
- eine Menge von Key-Value-Abbildungen
- eine Reihe von Funktionen, die Key-Value-Abbildungen akzeptieren
- eine Verteilfunktion zum Aufruf der gewünschten Funktion
Verwendung beider Paradigmen abhängig vom Anwendungskontext und persönlichem Geschmack
Aufwand der Erweiterbarkeit der Paradigmen sollte ebenfalls in Betracht gezogen werden

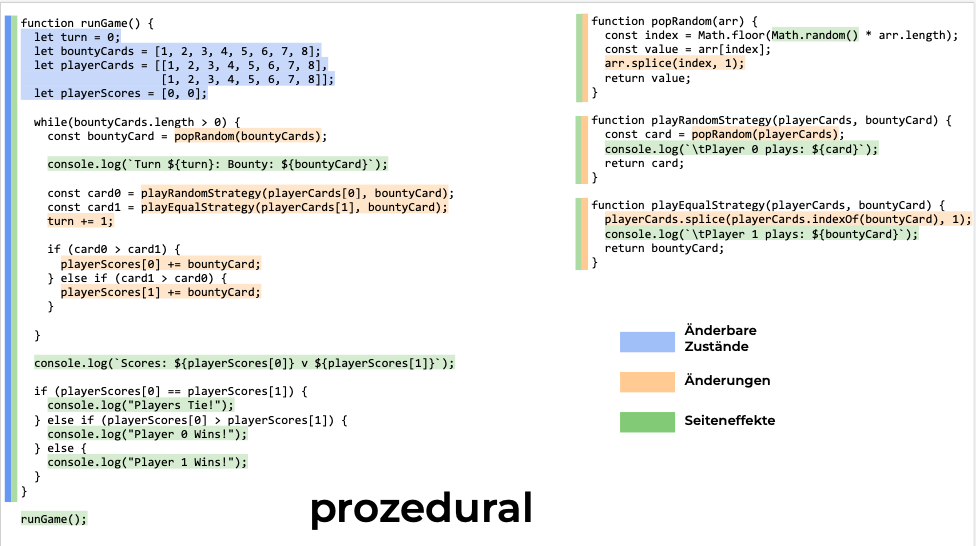
Objektorientiert vs. Prozedural vs. Funktional

Objektorientiert

Prozedural

Funktional

Funktionale Entwurfsmuster

Command-Pattern
- Modularisierung von Befehlen und Aufrufen
Strategy-Pattern
- Flexibler Wechsel von alternativen Verhalten
Oberserver-Pattern
- Benachrichtigung einer oder mehrerer Objekte, wenn sich der Zustand eines bestimmten Objekts ändert

6. Funktionale Konzepte in Java

Gilt nur für Java 8 oder größer!

z.B. map, filter und reduce
Vermeidung expliziter Mutation
lesbarer Code
Formulierung was (deklerativ) geschehen soll, nicht wie (imperativ)
Objektorientierung steht nicht im Widerspruch zur Funktionalen Programmierung

Funktionale Interfaces in Java

Consumer<T> - Operation ohne Rückgabe
Supplier<T> - Fabrik, die ein neues oder existierendes Objekt liefert
Predicate<T> - Prüfung einer Bedingung für ein Argument
Function<T> - Operation mit Resultat

Fluent Interfaces

Objektorientierte API unter Verwendung von method chaining

Verwendung von Fluent Interfaces am Beispiel:

public static void main(final String[] args) {
	FluentMailer.send(mailer ->
		mailer.from("build@agiledeveloper.com")
			.to("venkats@agiledeveloper.com")
			.subject("build notification")
            .body("...much better..."));
  }

7. Relationale Programmierung

Logische Programmierung

Häufig als “Erweiterung” der relationalen Programmierung betrachtet

Definition von Prädikaten
kürzer als Funktionale Programmierung
vielseitiger verwendbarer als Funktionen

Code-Beispiel: (Prolog)

natural(z).
natural(s(N)):- natural(N).

% Beispiel "plus"
plus(z, N, N):- natural(N).
% Definition von Variablen durch Großbuchstaben
plus(s(N), M, s(X)):- plus(N, M, X).

% Definition von beliebigen Variablen durch "_"
print(_).

8. Relational-logische Programmierung

Relational-logische Programmierung: Programme spezifizieren Relationen und Größen
Logische Programmierung: Programm mit Datenstrukturen (Listen, Bäumen etc.)
Verwendung von Prädikaten
Ziel ist die Beantwortung der Variablenbelegung durch
- Unifikation: Belegung der Variablen zweier Terme, so dass sie gleich sind
- Backtracking: Suchstrategie zur Beweisfindung
Es gibt keine Typen

Prolog

Alle Daten werden durch Terme repräsentiert
Term:
- Atom (Bsp: hans)
- Variable (Bsp: X)
- Ganzzahl oder Gleitkommazahl
- zusammengesetzter Term (Bsp: f(a))
Prolog verwendet Tiefensuche fürs Backtracking
Reihenfolge der Klauseln ist entscheidend

Code-Beispiel: (Prolog)

vater(hans, paul).
vater(hans, anna).

% Abfrage
?-	vater(X,Y).
	X=hans;
	Y=paul; % weitere Abfrage durch Simikolon
	X=hans;
	Y=anna. % bei weiterer Abfrage würde "false." kommen

% Regel
% Hinweis: "," stehen für UND-Verknüpfungen
father(Dad, Child) :- parent(Dad, Child), male(Dad).

% Listenoperationen
member(X, [X, Y, Z]).

append([A], [X, Y, Z]).

mapList(praed(3), [1, 2, 3], X).

count([],0).
% "|" entspricht cons
% "is" entspricht Zuweisung
count([_|Tail],N) :- count(Tail, X), N is X+1.

% Abfragen
?- count([a, b, c], N).
N = 3.
?- count([a, b, c], 3).
true.

Prädikat `cut` und `fail`

`cut`

Darstellung durch , !.

Verhindert das Backtracking
Wenn nur eine Regel erfüllt werden soll
Einsatzfälle:
- Effizienzsteigerung
- Speichereinsparung
- Verkürzung von Programmen
Cuts sind mit Vorsicht einzusetzen

`fail`

Darstellung durch , fail.

Das Prädikat fail schlägt immer fehl
Hierdurch wird immer Backtracking ausgeführt
Erreicht die Ausgabe aller möglichen Belegungen ohne Benutzerinteraktion (Anfrage durch “;”)

`Negation mit cut und fail`

Darstellung durch , !, fail.

Ausdrücken von Negationen durch die Verwendung von cut und fail

mag(karl, X) :- salami_pizza(X),!,fail.
mag(karl, X) :- pizza(X).

pizza(X)  :-  vier_jahreszeiten_pizza(X).
pizza(X)  :-  salami_pizza(X). 
pizza(X)  :-  champignon_pizza(X).

vier_jahreszeiten_pizza(vklein). 
vier_jahreszeiten_pizza(vgross). 
salami_pizza(s). 
champignon_pizza(c).

?- mag(karl,c).
true.

?- mag(karl,s).
false.

Probleme

Die Regeln dürfen nicht vertauscht werden
mag(karl, X) liefert false

Besser als `cut and fail`:

Negation

neg(Ziel)  :-  Ziel,!,fail. 
neg(Ziel).

mag(karl, X) :- pizza(X), neg(salami_pizza(X)).

9. Constraint Programmierung - Grundlagen

“Regelbasierte” Programmierung
Keine definition eines Algorithmus
Das Programm versucht den Zustand zu finden, in dem die Regeln erfüllt sind
Anwendungsgebiete:
- Erstellung von Stundenplänen
- Entscheidungsunterstützungssysteme für Planung und Konfiguration
- Konsistenzsicherung in Datenbanksystemen

Constraint

Beziehung zwischen verschiedenen Variablen
Constraints beschreiben Wissen über die Werte der Variablen
Beispiel aus dem Alltag: Terminabsprachen

Constraint-satisfaction

verwendet kombinatorische Methoden
- systematische Suche
- Generate & Test (Belegung aller Variablen wird erzeugt und geprüft)
- Backtracking (Schrittweise Erweiterung korrekter Teillösungen zur Gesamtlösung)

Constraint-solving

verwendet mathematisch-analytische Verfahren
Bsp:
- Differentation
- Integration
- Taylor-Reihen

primitive Constraints

beschreiben einen Zusammenhang zwischen Größen
Bsp:
- (adder x y z)
- (multiplier x y z)
Constraints können durch Konnektoren verbunden werden
Konnektoren aktivieren alle verbundenen Constraint-Elemente nach Erhalt eines Werts

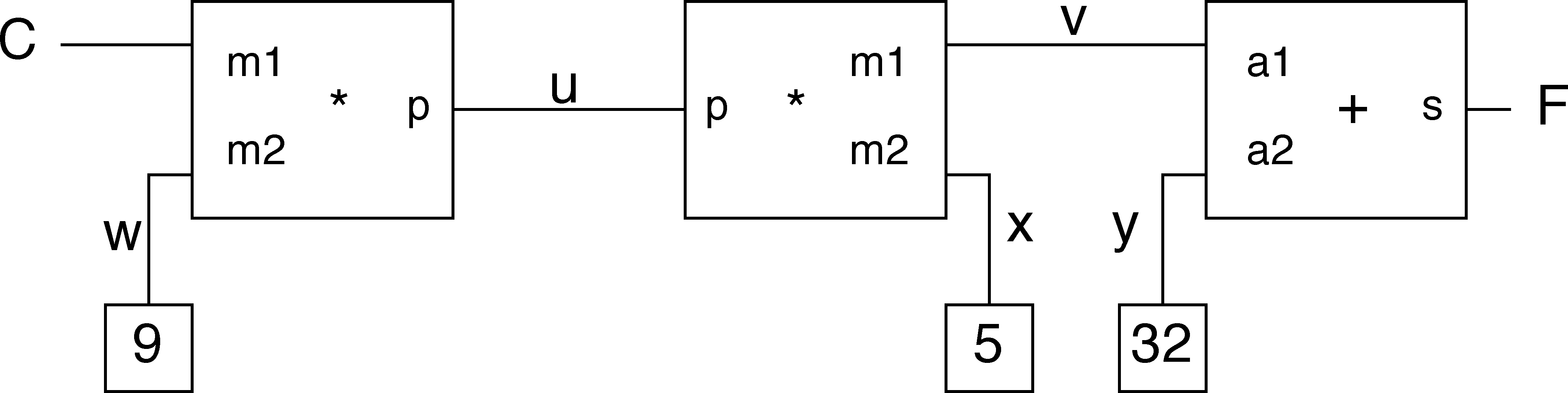
Beispiel von Konnektoren und Constraints

Celsius zu Fahrenheit Converter

Lösung in Clojure

(def celsius-fahrenheit-converter 
  (fn [c f]
    (let [u (make-connector)
          v (make-connector)
          w (make-connector)
          x (make-connector)
          y (make-connector)]
      (multiplier c w u)
      (multiplier v x u)
      (adder v y f)
      (constant 9 w)
      (constant 5 x)
      (constant 32 y)
      'ok)))

Lösung in Prolog

cf(C, F) :- {9*C=5*(F-32)}.

10. Constraint-logic Programmierung

Typisches Vorgehen
- 1. Analyse des Problems
- 1. Bestimmung der Bedingungen / Relationen
- 1. Formulierung der Bedingungen / Relationen
- 1. Lösung der Gleichungen
Typische Anwendungsgebiete
- Anwendungen mit häufig ändernder Problemspezifikation
- Anwendung mit benötigter Entscheidungsunterstützung
- Planung
- Ressourcen-Zuweisung
- Logistik / Transport
- Finanzwesen
- Navigation

11. Parallelprogrammierung

Einstieg

Nebenläufigkeit	Parallelität
mehrere unabhängige Aufgaben zur gleichen Zeit	Aufteilung einer Aufgabe in Teilaufgaben
Aufgaben konkurrieren um Ressourcen
Resultate einzelner Aufgaben beeinflussen evtl. das Verhalten anderer Aufgaben	Resultate einzelner Aufgaben beeinflussen nicht das Verhalten anderer Aufgaben
Nicht-Determinismus	Determinismus bleibt erhalten
Können Deadlocks verursachen
Können Raceconditions verursachen
Fehlverhalten schwer zu reproduzieren

Mehrkernprozessoren

gemeinsame Nutzung von Hauptspeicher und Takt
Erhöhung des Durchsatzes
höhere Zuverlässigkeit

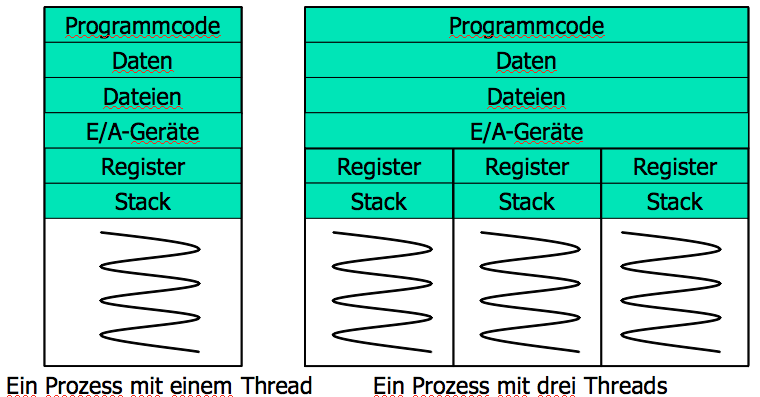
Prozesse und Threads

Prozess	Thread
Programm in der Ausführung	Ausführungsstrang eines Prozesses
benötigt Ressourcen (Speicher, Prozessor, Dateien etc.)	benötigt Prozessor und eigenen Stack
	verwendet Programmcode, Dateien etc.
	mehrere Threads in einem Prozess möglich

Multithreading

Beispiele
- Anwendungen mit grafischer Oberfläche
- Serversoftware (Webserver, DB-Server)
Vorteile:
- gemeinsame Nutzung von Ressourcen
- kurze Antwortzeiten
- geringer Aufwand

Multithreading (in Java)

Threads verursachen geringere Kosten als Prozesse
Umschalten zwischen Prozessen kostet viel Rechenzeit
Programmierer müssen Race Conditions und Deadlocks verhindern

Problem des überlappenden Aufrufs von Operationen

Thread muss seine Operation ohne Unterbrechung beenden können
Threads müssen synchronisiert werden
Mutual Exclusion: Wechselseitiger Ausschluss
Sperrmechanismen:
- Semaphoren
- Mutex (Semaphore mit dem Wert 1 - stellt Mutual Exclusion sicher)
- Monitor (stellt wechselseitigen Ausschluss sicher und stellt Mechanismen für Thread-Kooperationen bereit) [Bsp. Java synchronized]

class Test {
    static int n;
    static Object lock = new Object();
    void incrementN() {
        synchronized(lock) {
            n = n + 1;
        }
    }
}

Threadsichere Typen in Java

In Java gibt es Threadsichere Datentypen. Bsp:

java.util.concurrent.atomic
- AtomicInteger
- AtomicBoolean
- etc.
java.util.concurrent.ConcurrentHashMap
java.util.concurrent.CopyOnWriteArrayList
java.util.concurrent.BlockingQueue
etc.

Software Transactional Memory

Konzept paralleler Berechnungen, die auf gemeinsame Arbeitsspeicherbereiche zugreifen
Ziel: Ausführungsgeschwindigkeit steigern

Parallele Algorithmen

Parallelisierung von Algorithmen zur besseren Effizienz
Benötigt eine geeignete Parallelisierungsstrategie
Funktion höherer Ordnung map als ideales Beispiel zur Parallelisierung
Beispiel in Java: Parallelsort

1. Programmierparadigmen

Was ist ein Programmierparadigma?

Programmierstile:

Zuordnung:

Prozedurale- vs. Objektorientierte Programmierung

2. Typsysteme

Datentyp:

Zweck von Typisierung:

Typsysteme

Statische vs dynamische Typisierung

Strenges vs schwaches Typsystem

Explizites vs implizites Typsystem

Übersicht Typsysteme

Funktionale Programmiersprachen

Clojure

REPL (Read-Eval-Print-Loop)

Beispiel-Code

Standard ML

Beispiel-Code:

3. Ausdrucksmittel funktionaler Programmiersprachen

Datentypen

Pattern Matching

Verwendung von Pattern Matching

Beispiel-Code:

Curryfizierung - partielle Anwendung

Partielle Anwendung:

Clojure

Grundlagen:

Beispiel-Code:

4. Ausgewählte Kapitel

Datenabstraktion

Metazirkulärer Interpreter

Lazy evaluation

Funktionale Datenstrukturen

Beispiel

5. Funktionale- vs. Objektorientierte Programmierung

Zusammenfassung:

Objektorientiert vs. Prozedural vs. Funktional

Objektorientiert

Prozedural

Funktional

Funktionale Entwurfsmuster

Command-Pattern

Strategy-Pattern

Oberserver-Pattern

6. Funktionale Konzepte in Java

Funktionale Interfaces in Java

Fluent Interfaces

Verwendung von Fluent Interfaces am Beispiel:

7. Relationale Programmierung

Logische Programmierung

Code-Beispiel: (Prolog)

8. Relational-logische Programmierung

Prolog

Code-Beispiel: (Prolog)

Prädikat cut und fail

cut

fail

Negation mit cut und fail

Probleme

Besser als cut and fail:

9. Constraint Programmierung - Grundlagen

Constraint

Constraint-satisfaction

Constraint-solving

primitive Constraints

Beispiel von Konnektoren und Constraints

Lösung in Clojure

Lösung in Prolog

10. Constraint-logic Programmierung

11. Parallelprogrammierung

Einstieg

Mehrkernprozessoren

Prozesse und Threads

Multithreading

Multithreading (in Java)

Problem des überlappenden Aufrufs von Operationen

Threadsichere Typen in Java

Software Transactional Memory

Parallele Algorithmen

Prädikat `cut` und `fail`

`cut`

`fail`

`Negation mit cut und fail`

Besser als `cut and fail`: